- Last edited on June 23, 2025
Critical Appraisal and Statistics
Primer
Critical Appraisal is the process of carefully and systematically assessing the outcome of scientific research (evidence) to judge its trustworthiness, value, and relevance in a particular clinical context. When critically appraising a research study, you want to think about and comment on:
- How solid is the rationale for the research question?
- How important is the research question?
- What is the potential impact of answering it? (clinically, research, health policies, etc…)
- Can I trust the results of this research?
Having a systematic approach to critically appraising a piece of research can be helpful. Below is a guide.
Before You Begin... Read This Section First
Introduction to Statistics and EpidemiologyErrors and Biases
Random Error vs. Systematic Error (Bias)
Random error is an error in a study that occurs due to pure random chance. For example, if the inherent prevalence of depression is 4%, and we do a study with sample size of 100 examining the prevalence of depression, the study could by pure random chance have 0 people with people depression even though the prevalence is 4%. Increasing the sample size decreases the likelihood of random errors occuring, because increases your power to detect findings.
Systematic error is also known as bias. This is an error in the design, conduct, or analysis of a study that results in a mistaken estimate of a treatment's or exposure's effect on the risk or outcome of a disease. These errors can distort the results of a study in a particular direction (e.g. - favouring a medication treatment, or not favouring a treatment).
The Eternal Challenge in Medical Research
The challenge in any research is to design a study with adequate control over the two major threats to the results of a study: random error and systematic error. The failure to account for these errors, or reading a published study's results and not accounting for these errors is the most common problem affecting research today.Bias
Systematic errors (i.e. - biases) can threaten the validity of a study. There are two types of validity:
- External Validity: How generalizable are the findings of the study to the patient you see in front of you
- Internal Validity: Is the study actually measuring and investigating what it set out to do in the study?
There are many types of biases, and some of them are listed out in the table below. Researchers also use more comprehensive tools to measure and assess for bias. The most commonly used tool is the Cochrane Risk of Bias Tool. The components of the Cochrane Risk of Bias Tool is not described here.
Examples of Biases
| Type of Bias | Definition | Example | How To Reduce This Bias |
|---|---|---|---|
| Sampling Bias | When participants selected for a study are systematically different from those the results are generalized to (i.e. - the patient in front of you). | A survey of high school students to measure teenage use of illegal drugs does not include high school dropouts. | Avoid convenience sampling, make sure that the target population is properly defined, and that the study sample matches the target population as much as possible. |
| Selection Bias | When there are systematic differences between baseline characteristics of the groups that are compared. | A study looking at a healthy eating diet and health outcomes. The individuals who volunteer for the study might already be health-conscious, or come from a high socioeconomic background. | Randomization, and/or ensure the choice of the right comparison group. |
| Measurement Bias | The methods of measurements are not the same between groups of patients. This is umbrella term that includes information bias, recall bias and lack of blinding. | Using a faulty automatic blood pressure cuff to measure BP. See also: Hawthorne Effect | Use standardized, objective and previously validated methods of data collection. Use placebo or control group. |
| Information Bias | Information obtained about subjects is inadequate resulting in incorrect data. | In a study looking at oral contraceptive use (OCP) and risk of deep vein thrombosis, one MD fails to do a comprehensive history and forgets to ask about OCP use, while another MD does a very detailed history and asks about it. | Choose an appropriate study design, create a well-designed protocol for data collection, train researchers to properly implement the protocol and handling, and properly measure all exposures and outcomes. |
| Recall Bias | Recall of information about exposure to something differs between study groups | In a study looking at chemical exposures and risk of eczema in children, one anxious parent might recall all of the exposures their child has, while another parent does not recall the exposures in as much detail. | Could use records kept from before the outcome occurred, and in some cases, the keep exact hypothesis concealed from the case (i.e. - person) being studied. |
| Lack of blinding | If the researcher or the participant is not blind to the treatment condition, the assessment of outcome might be biased. | A psychiatrist tasked assessing whether a patient's depression has improved using a depression rating scale, but he knows the patient is on an antidepressant. He may be unconsciously biased to rate the patient as having improved. | Blind the participant/researcher. |
| Confounding | When two factors are associated with each other and the effect of one is confused with or distorted by the other. These biases can result in both Type I and Type II errors. | A research study finds that caffeine use causes lung cancer, when really it is that smokers drink a lot of coffee, and it has nothing to do with coffee. | Repeated studies; do crossover studies (subjects act as their own controls); match each subject with a control with similar characteristics. |
| Lead-time bias | Early detection with an intervention is confused with thinking that the intervention leads to better survival | A cancer screening campaign makes it seem like survival has increased, but the disease’s natural history has not changed. The cancers are picked up earlier by screening; but even early identification (with or without early treatment) does not actually change the trajectory of the illness. | Measure “back-end” survival (i.e. - adjust survival according to the severity of disease at the time of diagnosis). Have longer study enrollment periods and follow up on patient outcomes for longer. |
More Reading:
The Research Question
A research question that leads to a research study is often quite general, but the answer that we get from a published research study is actually extremely specific. As an example, as a researcher, I might want to know if a new SSRI is more effective than older SSRIs. This seems like an easy question to answer, but the reality is much more complicated. When looking at the results of a study, you want to think how specific or generalizable are the findings?
The Research Question
| The question I (the researcher) wish I could answer* | The question I'm actually answering I do the study | |
|---|---|---|
| Scope | General | Specific |
| Question | Is this newer antidepressant more effective the older antidepressant for people with depression? I want to know if it is a simple yes or no! | What proportion of depressed patients aged 18 to 64 with no comorbidities and no suicidal ideation and who have not been treated with an antidepressant experience a greater than 50% reduction in the Hamilton Rating Scale after 6 weeks of treatment with the new antidepressant compared to the old antidepressant? |
Study Population
Ask yourself, what is the target population in the research question? Then ask yourself, does the study sample itself actually represent this target population? Sometimes, the study sample will be systematically different from the target population and this can reduce the external validity/generalizability of the findings (also known as sampling bias). After this, you should look at the inclusion and exclusion criteria for the participants:
Inclusion/Exclusion Criteria
- Inclusion Criteria: specifies characteristics for the population that are relevant to the research question, for example, the study should detail the following about their participants:
- Age
- Diagnoses and medical conditions
- Medications
- Demographics
- Clinical Characteristics
- Geographic Characteristics
- Temporal Characteristics
- Exclusion Criteria: specifies subset of the population that will not be studied because of:
- High likelihood of being lost to follow-up
- Inability to provide good data
- High risk of side effects
- Unethical
- Any characteristic that has possibility of confounding the outcomes
Study Design
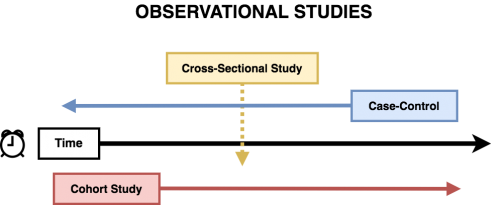
Different study designs have different limitations. Having an understanding of each type of common study design is an important part of critically appraising a study. The most common study designs in psychiatric research are experimental designs, such as randomized controlled trials, and observational studies, including: cross-sectional, cohort, and case-control.
Comparison of Common Study Types
| Description | Measures you can get | Sample study statement | |
|---|---|---|---|
| Randomized Control Trial (RCT) | A true experiment that tests an experimental hypothesis. Neither the patient nor the doctor knows whether the patient is in a treatment or control (placebo) group. | • Odds ratio (OR) • Relative risk (RR) • Specific patient outcomes | “Our study shows Drug X works to treat Y condition.” |
| Cross-Sectional | • Assesses the frequency of disease at that specific time of the study | • Disease prevalence | “Our study shows that X risk factor is associated with disease Y, but we cannot determine causality.” |
| Case-Control | • Compares a group of individuals with disease to a group without disease. • Looks to see if odds a previous exposure or a risk factor will influence whether a disease or event happens | • Odds ratio (OR) | “Our study shows patients with lung cancer had higher odds of a smoking history than those without lung cancer.” |
| Cohort | • Cohort studies be prospective (i.e. - follows people during the study) or retrospective (i.e. - the data is already collected, and now you're looking back). • Compares a group with an exposure or risk factor to a group without the exposure. • Looks to see if an exposure or a risk factor is associated with development of a disease (e.g. - stroke) or an event (e.g. - death). | • Relative risk (RR) | “Our study shows that patients with ADHD had a higher risk of sustaining traumatic brain injuries that non-ADHD patients.” |
Randomization Controlled Trials
Randomized Control Trials (RCTs) allows us to do a true experiment to test a hypothesis. Randomization with sufficient sample sizes, that both measurable and unmeasurable variables are even distributed across the treatment and non-treatment groups. It also ensures that reasons for assignment to treatment or no treatment are not biased (avoids selection bias).
- Check if randomization (of measured factors) was achieved – look at the demographics table (Table 1) to see if both groups seem similar. (However, just because the p value is > 0.05 does not mean randomization was successful)
- Check if blinding to the treatment or placebo was successful, ideally all of the people below should not be aware of which treatment the participant is getting, including:
- The researcher who allocates participants to treatment groups (avoids selection bias)
- Patients in the study (avoids desirability bias)
- Care providers (avoids subconsciously managing patients differently)
- Assessors (avoids measurement bias)
Blinding is of course not always possible (e.g. - an active medication may have a very obvious side effect that a placebo doesn't have, making it very obvious to the participant if they are on a placebo or not). One needs to understand potential impact of the breaking of the blind in these studies. Some studies may therefore implement active placebos rather than inert placebos, to counter this potential bias.[1]
What Are the Limitations of RCTs?
Although the core strength of RCTs is that it uses randomization to ensure a balance between groups in RCTs, it cannot ensure that outcomes are representative of a given population. For example, RCTs for patients with cancer represent less than 5% of U.S. adults with cancer.[2] Patients in RCTs also tend to be younger, healthier, and less diverse than real-world populations. This means the study findings from an RCT are not always generalizable to the patient that you have in front of of! Thus, the smart clinician must take in not just RCT evidence, but also real-world study data (such as observational studies).Why Do We Even Need a Control/Placebo Group Anyways?
Why do we need a placebo or control group in an RCT? In non-RCTs, there are many factors that can affect a therapeutic response, including:- Regression to the mean: on repeated measurements over time, extreme values or symptoms tend to move closer to the mean (i.e. - people tend to get better over time, especially in psychiatric disorders such as depression and anxiety).
- Hawthorne Effect: participants have a tendency to improve based on being in clinical trial, because they are aware they are being observed.
- Desirability Bias:patient/rater wanting to show that treatment works
The presence of a placebo or control group can adequately account for these confounding factors.
More Reading
- Control Groups
- Regression Towards The Mean
- Blinding
Randomization
Why are clinical studies so obsessed with randomization and randomized control trials (RCTs)? Randomization allows us to balance out not just both known biases and factors, but more importantly, unknown biases and risk factors. Randomization saves us from the arduous process of needing to account for every single possible bias or factor in a study. For example, in a study looking at the effectiveness of an antidepressant versus a placebo, a possible bias that might affect the result could be might be gender or other medication use (something you can measure). Of course, you try to skip randomization, and try to divide the groups equally amongst gender and medication use by yourself. However, unmeasurable factors (like family support, resiliency, genetics) might also affect a participant's response to medications.
Randomization is Hard
Sometimes, “randomized” samples aren't actually random because of biases as previously mentioned. Sometimes, sample are just straight up non-random (e.g. - a convenience sample, where you just find the easiest group to contact or to reach).The beauty of a properly done randomization is you can eliminate (or come close to eliminating) all the unknown factors. This way, you can be sure that the outcomes of your study are not affected by these factors since randomization should equally distribute all known and unknown factors amongst all treatment groups. Randomization is most effective when sample sizes are large. When studies have small sample sizes, they are called underpowered studies, which makes it hard to ensure the sample has been adequately randomized.
Observational Studies
Observational Studies are studies where researchers observe the effect of a risk factor, medical test, treatment or other intervention without trying to change who is or is not exposed to it. Thus these studies do not have randomization and do not have control groups. Observational studies come in several flavours, including cross-sectional, cohort, and case-control studies.
Cross-Sectional
- Good for obtaining a prevalence of a disease or condition
- e.g. - Point prevalence: at one specific point in time
- e.g. - Period prevalence: within 1 month period, within 12 month period
- You cannot infer causality from cross-sectional studies, only associations
- There is a risk for sampling Bias because you have no control over who is being measured at this specific point in time
Case-Control
Case-control studies (also known as retrospective studies) are studies where there are “cases” that already have the outcome data (e.g. - completed suicide, diagnosis of depression, diagnosis of dementia), and “controls” that do not have the outcome (hence the name case-control). Rather than watch for disease or outcome development, case-control studies look for and compare the prevalence of risk factors that lead to the outcome happening. For example, a research might look at antidepressant use, and whether that affects the outcome they already know (e.g. - cases of completed suicides)
- Case-control studies are always retrospective (looking into the past!)
- Rather than watch for outcome (i.e. - disease development), compare prevalence of risk factors
- “Cases” have the outcome (i.e. - completed suicide, dementia diagnosis, depression diagnosis); “controls” do not
- Since you already have selected a predetermined number of people with and without the disease, you cannot calculate a relative risk (RR). However, you can calculate an odds ratio (OR).
- Advantages:
- This is the only way to study rare diseases, since you already know how many cases there are!
- It is inexpensive because it invariably uses pre-existing data
- Weaknesses:
- Highly susceptible to different types of bias:
- Sampling bias
- You want to make sure that cases are not “atypical” presentations of a disease
- To mitigate this: try to include all cases that are a representative sample of the population
- Selection bias
- You need to make sure that the outcome cases are relatively similar to controls other than on the exposure. Otherwise, the controls might never even have been exposed to the risk factor or have very little chance of developing the outcome!
- To mitigate this: Select controls from same population as cases, match cases and controls on key variables, and have multiple control groups
- Recall bias
- The outcome cases more likely to remember an exposure than the controls (e.g. - asbestos and lung cancer)
- To mitigate this: use records kept from before the outcome occurred, and in some cases, the keep exact hypothesis concealed from the case (i.e. - person) being studied
Case-non-case
Cohort
A cohort study (also known as a prospective study) follows a group of subjects over time.
- It is the only way to describe incidence (incidence = number of new cases/time)
- It is a little better for inferring causality, but can take a long follow up time, and you need a large sample size
- Unlike a case-control study, you can also calculate a relative risk (RR) of a given outcome (i.e. - you can compares outcome between 2 groups who differ on a certain risk factor)
- Usually you have an exposure or a risk factor (e.g. - antidepressant) plus an outcome (e.g. - dementia)
- However, since you can't control who gets exposed top what, there is a high risk for selection bias!
- e.g. - those who take antidepressants might have more severe depression than those who do not
- e.g. - depression might be a confounding factor for dementia
- When looking at cohort studies, it is important to pay attention to the demographics table (“Table 1”), and look for selection bias and important confounding factors. Also try to think of other factors that might not have been measured in the study. This is an important issue with retrospective studies (relative to RCTs), since researchers do not have control over what was measured!
Key Difference Between Cohort and Case-Control Studies
- In cohort studies, the participant's groups are classified according to their exposure status (whether or not they have the risk/exposure factor). Cohort studies follow an exposure over time and looks to see whether it will cause disease. You can calculate a relative risk (RR).
- In case-control studies, the different groups are identified according to their already known health outcomes (whether or not they have the disease). You already know who has what disease, and are now travelling back in time to find out what risk factors may have played a role. You can only calculate an odds ratio (OR), and cannot calculate an RR from a cohort study.
Open Label
National Registers
Systematic Reviews and Meta-Analyses
Systematic Reviews (SR) and Meta-Analyses (MA) synthesize all the available evidence in the scientific literature to answer a specific research question. Systematic reviews describes outcomes of each study individually (always look for a forest plot in the paper). The meta-analysis is an extension of a systematic review that uses complex statistics to combine outcomes (if outcomes of different studies are similar enough). In most meta-analyses, there are usually strict criteria for study inclusion that usually weeds out flawed research study. However, this is not always the case! Poor study selection can often result in flawed meta-analysis findings (garbage in = garbage out)! It is also important to watch for publication bias (i.e. - certain articles might be favoured over others).
Network Meta-Analyses
Bayesian
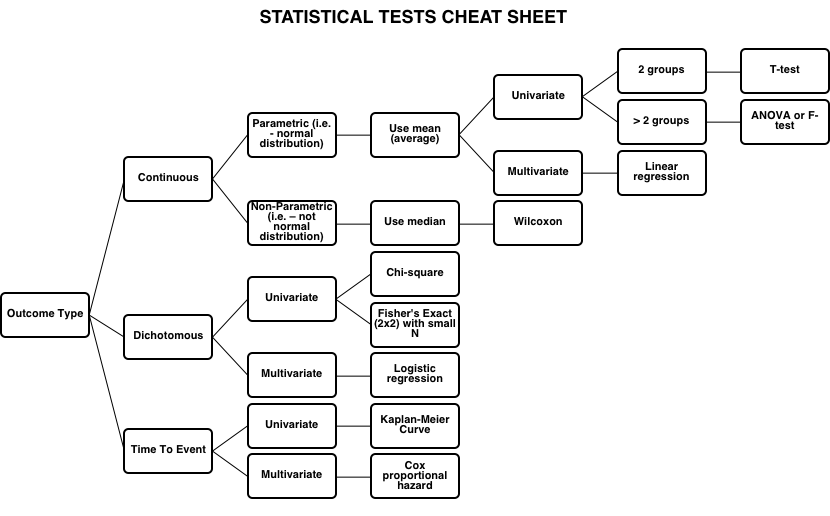
Statistical Tests
Cheat Sheet
Statistical Significance
p Values
Manipulating the Alpha Level Cannot Cure Significance Testing
We argue that making accept/reject decisions on scientific hypotheses, including a recent call for changing the canonical alpha level from p = 0.05 to p = 0.005, is deleterious for the finding of new discoveries and the progress of science. Given that blanket and variable alpha levels both are problematic, it is sensible to dispense with significance testing altogether. There are alternatives that address study design and sample size much more directly than significance testing does; but none of the statistical tools should be taken as the new magic method giving clear-cut mechanical answers. Inference should not be based on single studies at all, but on cumulative evidence from multiple independent studies. When evaluating the strength of the evidence, we should consider, for example, auxiliary assumptions, the strength of the experimental design, and implications for applications. To boil all this down to a binary decision based on a p-value threshold of 0.05, 0.01, 0.005, or anything else, is not acceptable.[3]Effect Sizes (Cohen's d)
- This is what you will often see in an RCT to illustrate the magnitude of an effect
- Can just mean a difference between means, or it can be standardized (e.g. Cohen’s d = difference between means/SD)
- Often described as small, medium or large
- For Cohen’s d: 0.2 is small, 0.5 is med, > 0.8 is large
Poor Statistical Methodologies
Results
Results Section
Depending on the design of the study, the results section will look very different. However, all studies should:
- Describe the sample (prevalence, incidence, and a “Table 1” of demographics)
- Show the relationships between factors (e.g. - treatment and outcome, risk factor and outcome)
- Tell you how large was a treatment effect (if looking at this)
Results: Means
Results may first compare the mean (average) between a treatment or non-treatment group:
- T-test, F-test (ANOVA): if p<0.05, then there is a significant difference
- See this in your “Table 1s” and in primary analysis of RCT outcomes
- If making multiple comparisons (tests) then you increase the chance that there will, by chance, be a significant result that is a false positive (Type I error), you can adjust for this using the Bonferroni correction.
Results: Risk
Results can be expressed in a number of ways, including:
- Absolute Risk Reduction (ARR)
- Relative Risk
- Relative Risk Reduction
- Number Needed To Treat (NNT)
- Number Needed to Harm (NNH)
How Might The Results Be Misleading?
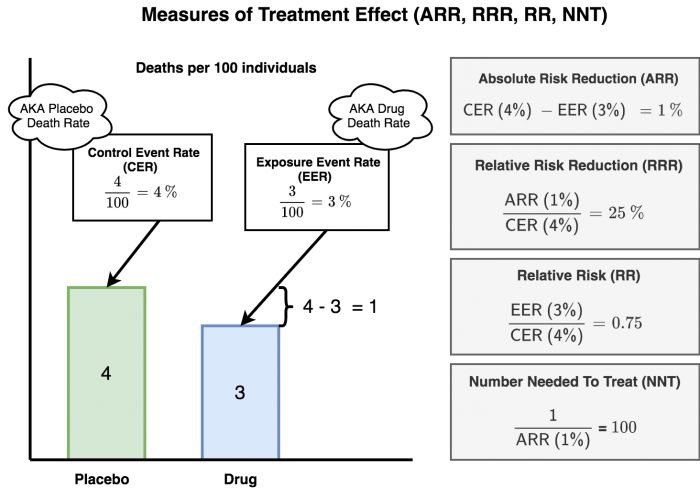
- Let's say a drug company is investigating a drug to prevent deaths after a heart attack. After the study of 1,000 participants, they find out that 4 people died in the placebo/control arm, and only 3 people died in the drug arm.
- If you calculate the relative risk reduction (RRR), it is 25% (1 ÷ 4 = 0.25)
- If however, you calculate the absolute risk reduction (ARR), it is only 0.1% (1 ÷ 1000 = 0.001)!!
- A drug company might be inclined publish the relative risk and relative risk reduction to make the benefits look great (Wow! We can advertise a 25% reduction in deaths!). On the flip aside, they might want to market side effects by expressing it in absolute risks instead (to make it seem much less). So you might read an article that Drug A will lower the risk of deaths by 25% (over-selling the drug) and the risks of developing side effects is very small (under-estimating the side effects).
- One should always express the risk in absolute and avoid percentages. So if the absolute risk reduction with this new drug is 0.1%, it means you need to treat 1,000 people with the drug to prevent 1 death. Does not sound as great as a drug that “reduces mortality by 25%”, now does it? Always get the ABSOLUTE!
</WRAP>
Example
Example: You are studying a medication to reduce the risk of death from heart attacks. 4% died in the control group. 3% died in the treatment group. This was a 1 year study. See figure 3 for a visualization of the calculations.Measuring Treatment Effect
| Measure | Calculation* | Example |
|---|---|---|
| Control Event Rate (CER) | (development of condition among controls) ÷ (all controls) | 4% as per above example |
| Experimental Event Rate (EER) | (development of condition among treated) ÷ (all treated) | 3% as per above example |
| Absolute Risk Reduction (ARR) | CER (risk in control group) - EER (risk in treatment group) | 4%-3% = 1% absolute reduction in death |
| Relative Risk (RR), aka Risk Ratio (RR) | EER (risk in treatment group) ÷ CER (risk in control group) | 3% ÷ 4% = 0.75 (the outcome is 0.75 times as likely to occur in the treatment group compared to the control group). The RR is always expressed as a ratio. |
| Relative Risk Reduction (RRR) | ARR ÷ CER (risk in control group) | 10% ÷ 40% = 25% (the treatment reduced risk of death by 25% relative to the control group) |
| Number Needed to Treat (NNT) | 1 ÷ (ARR) | 1 ÷ 10% (i.e. 1 ÷ 0.1) = 10 (we need to treat 10 people for 1 years to prevent 1 death) |
Relative Risk (RR)
Relative Risk (RR) is a ratio of the probability of an outcome in an exposed group compared to the probability of an outcome in an unexposed group
- Dichotomous variables can offer relative risk calculations of an event happening (i.e. - risk in group 1 relative to risk in group 2)
- RR is used for cohort studies, and randomized control trials
- RR tells us how strongly related 2 factors are but says nothing about the magnitude of the risk.
- If RR = 1, then both groups have equal risk
Interpreting Relative Risk (RR)
| RR = 1 | No association between exposure and disease |
|---|---|
| RR > 1 | Exposure associated with ↑ disease occurrence |
| RR < 1 | Exposure associated with ↓ disease occurrence |
Relative Risk Reduction (RRR)
Relative risk reduction (RRR) measures how much the risk is reduced in the experimental group compared to a control group. For example, if 50% of the control group died and 25% of the treated group died, the treatment would have a relative risk reduction of 0.5 or 50% (the rate of death in the treated group is half of that in the control group).
Absolute Risk Reduction (ARR)
Absolute Risk Reduction (ARR) is the absolute difference in outcome rates between the control and treatment groups (i.e. - CER - EER). Since ARR does not involve an explicit comparison to the control group like RRR, it does not confound the effect size of the treatment/intervention with the baseline risk.
Number Needed to Treat (NNT)
Number Needed to Treat (NNT) is another way to express the absolute risk reduction (ARR). NNT answers the question “How many people do you need to treat to get one person to remission, or to prevent one bad outcome?” To compare, a RR and RRR value might appear impressive, but it does not tell you how many patients would you actually need to treat before seeing a benefit. The NNT is one of the most intuitive statistics to help answer this question. In general a NNT between 2-4 means there is an excellent benefit (e.g. - antibiotics for infection), NNT between 5-7 is associated with a meaningful health benefit (e.g. - antidepressants), while NNT >10 is at most associated with a small net health benefit (e.g. - using statins to prevent heart attacks).[4]
Odds Ratio (OR)
- Odds Ratio = odds that a case is exposed/odds that a case is not exposed
- Used for case-control studies because there is no way to compute the risk of the outcome (i.e. - because you started with the outcome already)
- Very frequently used because it is the output of a logistic regression
- The OR approximates the RR for rare events (but becomes very inaccurate when used for common events!)
- Note that as a rule of thumb, if the outcome occurs in less than 10% of the unexposed population, the OR provides a reasonable approximation of the RR.
- If OR = 1, then equal odds for both exposed and non-exposed groups (lower bound is 0)
Interpreting Odds Ratio (OR)
| OR > 1 | Means there is greater odds of association with the exposure outcome |
|---|---|
| OR = 1 | Means there is no association between the exposure and outcome |
| OR < 1 | Means there is lower odds of association with the exposure outcome |
OR vs. RR
OR vs. RR
| High Pesticides | Low Pesticides | |
|---|---|---|
| Lukemia (Yes) | 2 (a) | 3 (b) |
| Lukemia (No) | 248 (c) | 747 (d) |
| Total | 300 (a+c) | 750 (b+d) |
- Relative Risk (RR) = (incidence in exposed) ÷ (incidence in unexposed)
- = a/(a + b) ÷ c/(c + d)
- = 2/(2 + 248) ÷ 3/(3 + 747)
- RR = 2.0
- Odds Ratio (OR) = (odds of exposure among cases) ÷ (odds of exposure among controls)
- = (a ÷ c) ÷ (b ÷ d)
- = (a × d) ÷ (b × c)
- = (2 × 747) ÷ (3 × 248)
- OR = 2.0080645161 = 2.01
Note that even though RR and OR both = 2, they do not mean the same thing!
- An OR = 1.2 = there is a 20% increase in the odds of an outcome (not risk) with a given exposure
- An OR = 2.0 = there is a 100% increase in the odds of an outcome (not risk) with a given exposure
- This can also be stated that there is a doubling of the odds of the outcome (e.g. - high pesticides exposure are 2 times as likely to have lukemia)
- Note, this is not the same as saying a doubling of the risk (i.e. - RR = 2.0)
- An OR = 0.2 means there is am 80% decrease in the odds of an outcome with a given exposure
Hazard Ratios (HR)
In psychiatry, studies may typically look at the time to relapse for an event (e.g. - time until a depressive episode relapse). There are several “buzz words” that may be used:
- Univariate analysis means there are Kaplan-Meier Curves
- Multivariable analyses most commonly use Cox proportional hazard modelling
- Both types of analyses allow for censoring
- Censoring allows for analysis of data when the outcome [dependent variable] has not yet occurred for some patients in the study
- e.g. - a 5-year study looking a diagnosis of dementia, but not all participants have dementia by the end of the 5-year study
- These analyses generate a “hazard ratio”, which is the ratio of:
- [chance of an event occurring in the treatment arm]/[chance of an event occurring in the control arm], or
- [risk of outcome in one group]/[risk of outcome in another group]… occurring over a given interval of time
Linear Regression
Linear regression generates a beta, which is the slope of a line
- Beta = 0 means no relationship (horizontal line)
- Beta > 0 means positive relationship
- Beta < 0 means negative relationship
Confidence Intervals (CI)
- Range of values within which the true mean of the population is expected to fall, with a specified probability.
- CI for sample mean = x ± Z(SE)
- The 95% CI (α = 0.05) is often used
- As sample size increases, CI narrows
- Remember:
- For the 95% CI, Z = 1.96
- For the 99% CI, Z = 2.58
Interpreting Confidence Intervals (CI)
| If the 95% CI for a mean difference between 2 variables includes 0… | There is no significant difference and H0 is not rejected |
|---|---|
| If the 95% CI for odds ratio (OR) or relative risk (RR) includes 1… | There is no significant difference and H0 is not rejected |
| If the CIs between 2 groups do not overlap… | A statistically significant difference exists |
| If the CIs between 2 groups overlap… | Usually no significant difference exists |
Causation
Most studies only demonstrate an association (e.g. - antidepressant use in pregnancy associated with an increased rate of preterm birth). How can we decide whether association is, in fact, causation? (e.g. -Does anti-depressant use in pregnancy actually cause preterm birth?). The Bradford Hill criteria, otherwise known as Hill's criteria for causation, are a group of nine principles that can be useful in establishing epidemiologic evidence of a causal relationship between a presumed cause and an observed effect
Bradford-Hill Criteria
- Experimental evidence: from a laboratory study and or RCT
- Researcher controls assignment of subjects and exposure
- Strength of Association: what is the size of relative risk or odds ratio (remember, RR or OR = 1 means no association)
- Consistency: same estimates of risk between different studies
- Gradient: increasing the exposure results in increasing rate of the occurrence
- Biological and Clinical Plausibility: judgement as to plausibility based on clinical experience and known evidence
- Specificity: when an exposure factor is known to associated only with the outcome of interest and when outcome not caused by or associated with other risk factors (e.g. - thalidomide)
- Coherence: also called “triangulation”: when the evidence from disparate types of studies “hang together”
- Temporality: realistic timing of outcome based on exposure
- Analogy: similar associations or causal relationships found in other relevant areas of epidemiology
Other Issues
Placebo Effect
Evidence-Based Medicine
Evidence-Based Medicine (EBM) typically will depend on the use of statistical and critical appraisal approaches. However, there are also inherent limitations and potential issues with the way EBM is applied in current medical research.